[자료구조] B- Tree , B+ Tree

B- Tree

B-Tree는 탐색 성능을 높이기 위해 높이를 균형있게 유지하는 Balanced Tree의 일종입니다.

B-Tree는 이진 트리와는 다르게 하나의 노드에 여러개의 데이터를 가질수 있으며, 두개 이상의 자식노드들을 가질 수 있습니다. 만약 노드의 자식 수 중 최대값이 K라면 이 B-Tree의 차수는 K차수라 하며 K차 B-Tree라고 합니다.

 

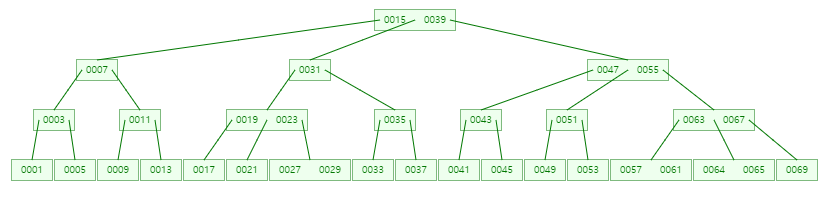
위의 그림은 3차 B-Tree이며 각 노드마다 최대 자식 수가 3개 인것을 확인 할 수 있습니다.

B-Tree는 하나의 노드에 여러 키를 배치하면서 이진트리보다 훨씬 많은 데이터를 담을 수 있으며, 노드 내의 데이터들은 항상 정렬된 상태입니다.

이러한 B-Tree는 다음과 같은 특징을 갖습니다.

• 각 노드의 데이터는 정렬되어 있습니다.
• 모든 leaf node는 같은 레벨에 있습니다.
• K차 트리일때 루트 노드와 leaf 노드를 제외한 노드들은 최소 [K/2], 최대 K개의 서브 트리를 갖습니다.
• 노드의 키는 최소[K/2]-1, 최대 K-1개를 갖을 수 있습니다.
• 모든 leaf 노드들은 같은 level에 있어야 합니다.

시간복잡도

B-Tree를 이용하는 이유중 하나는 시간복잡도 문제 입니다.

일반적인 트리의 경우 평균적으로 O(logN)의 시간복잡도를 갖지만, 트리가 편향된 최악의 경우O(N)의 시간복잡도를 갖게 됩니다. 하지만 B-Tree는 Balanced Tree로서 항상 같은 leaf 노드들이 같은 레벨에 존재하기 때문에 최악의 경우에도 O(logN)의 시간복잡도가 보장됩니다.

B+ Tree

B+Tree는 B-Tree의 몇가지 문제점을 보완한 트리로, 가장 큰 차이점은 B+ Tree에서는 데이터를 저장하는 leaf노드만이 실제로 데이터를 갖고있고, 내부 노드들은 단순히 키값만을 갖고 있게 됩니다. 반면 B-Tree는 내부 노드와 leaf노드 모두 데이터를 가질 수 있습니다. 아래 그림을 보면 모든 leaf node들은 연결리스트로 연결되어 있습니다.

 

이러한 차이점으로 B+Tree는 다음과 같은 이점이 있습니다.

• 데이터를 순차적으로 저장하고 검색할 수 있어서 디스크 I/O 작업을 줄일 수 있습니다.
• 리프 노드에서만 데이터를 저장하므로, 내부 노드에서 데이터를 찾는 작업을 생략할 수 있습니다. 이는 검색 시간을 단축시키는 데 도움이 됩니다.
• 리프 노드끼리 연결 리스트 형태로 구성되어 있어서 범위 검색(range query)을 쉽게 할 수 있습니다.

B+Tree의 내부노드는 인덱스 노드라고 불리며, leaf노드는 데이터 노드라고 불립니다.

인덱스 노드의 value값에는 다음 노드를 가리키는 포인터 주소가 존재하며, 데이터 노드의 value값에는 데이터가 존재하게 됩니다. 따라서 키값은 중복될 수 있고(인덱스 노드와 데이터 노드가 동일한 키값을 소유할 수 있음), 데이터 검색을 위해서leaf노드까지 내려가야 한다는 특징이 있습니다.

 

아래에서 B Tree를 직접 생성해가며 익힐 수 있습니다.

B-Tree -> https://www.cs.usfca.edu/~galles/visualization/BTree.html

B+Tree -> https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

 

 

 

참고자료

https://siahn95.tistory.com/128?category=821999 

[DB] 인덱스란? - (2) 구조, B-Tree 계열을 쓰는 이유